Function transforms (providing a broader picture of Laplace Transforms)

I’ll begin this article by brushing up a few definitions:

A function is a mapping between two sets: the domain D and the codomain C.

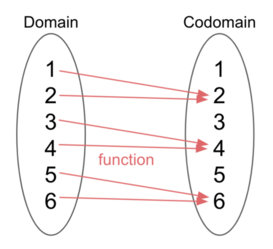
It’s very important to note here that the function is the mapping itself, and not an element in the codomain or the domain. The function operates on an element in the domain to give an element in the codomain. Formally, we would write this function as $f:D\to C$

I’ll also brush up on what a Vector Space is: a vector space $V$ is a set of vectors over a given field $F$ on which two operations (functions) are defined:

• $+:V\times V\to V$ - this is called Addition
• $\cdot :V\times F\to V$ - this is called Scalar Multiplication.

There are some other requisites of a vector space, such as the existence of an additive inverse and identity elements, but I won’t get into the nitty-gritties of those. Just keep in mind that addition and scalar multiplication over a vector space are closed.

Function Spaces

Suppose for a function $f:X\to V$, the codomain of a function is a vector space $V$ over $F$ ($X$ is the domain, which can be any set). Then, by definition, for any two elements $\overrightarrow{a},\overrightarrow{b}\in V$ and a scalar $k\in F$, $\overrightarrow{a}+\overrightarrow{b}\in V$ and $k\cdot \overrightarrow{a}\in V$.

Consider another function $g:X\to V$. Suppose now that for any $x\in X$, $f(x)=\overrightarrow{a}$ and $g(x)=\overrightarrow{b}$ for some $\overrightarrow{a},\overrightarrow{b}\in V$. Therefore, $\overrightarrow{a}+\overrightarrow{b}=f(x)+g(x)\in V$. We can define another function $(f+g)$ such that $(f+g)(x)=f(x)+g(x)$. Note that this is valid because V is a vector space, and because addition is closed under a vector space. The sum of two functions from $X\to V$ is also a function from $X\to V$!

Let’s try proving the same for scalar multiplication. For any $c\in F$, we have $c\cdot \overrightarrow{a}=c\cdot f(x)\in V$. Define $(c\cdot f)$ such that $(c\cdot f)(x)=c\cdot f(x)$. This is also a function from $X\to V$.

From the above two statements, we can see that the maps themselves are linear: that is, they can be added and scalarly multiplied, with the resulting map preserving the domain and codomain. We can thus say that the functions thus defined form a vector space themselves, which we call a function space. Note that there are a few more details involved, such as the existence of an identity function and an additive inverse. Similar to the additive/multiplicative proofs, these follow from the properties of the vector space. One interesting question to note is what if there is no function in the space that maps an element of $X$ to the identity element $\overrightarrow{0}$ of $V$? Would the resulting function space still be a vector space?¹

Function transformations

If function spaces behave like vector spaces, this begs the question: what’s the equivalent of linear transformations for function spaces? The equivalent is called a function transformation, and it converts a function $f:X\to V$ to another function $T(f)=F:Y\to W$. Note that if $f$ lies in a function space ${\mathcal{S}}_f$, then $F$ need not lie in a function space! Consider the counterexample $P(f)$ on $f:X\to V$, which maps all $x\in X$ to $1$. This is not a function space, as $F(x_1)+F(x_2)=2\notin 1$. We would need to prove the linearity of $F$ independently of $f$ being a function space. Note also that this particular transform doesn’t have an inverse. Transforms that are linear in nature generally have an inverse transform associated with them.

Some examples of function transformations include $Df=\frac{df}{dx}$ (the differential transform), as well as $I(f)={\int }_a^{b}fdx$, the integral transform. Note that these are both simple examples of transforms which preserve mapping, that is if $f:\mathbb{R}\to \mathbb{R}$ and f is differentiable on $\mathbb{R}$, then $Df:\mathbb{R}\to \mathbb{R}$ as well. An example of something that doesn’t preserve mapping would be the parameterization transform for a multivariate function: if we have $f:{\mathbb{R}}^{\mathbb{3}}\to \mathbb{R}$, then the parameterization transform $P(f(x,y,z))=F(x(t),y(t),z(t))=F(t)$ gives $F:\mathbb{R}\to \mathbb{R}$.

Integral transformations

Integral transformations are just one type of functional transform, but they’re the most used type of transform due to their usefulness. A general integral transform takes the form

$$I(f)={\int }_{x_1}^{x_2}K(s,x)f(x)dx$$

$K(s,x)$ is called the kernel of the integral transform, and the transform has different intuitive meanings depending on the kernel and the limits used. A full list of common kernels can be found at the Wikipedia page of Integral transforms. A few key things to note however are:

1. The integral transform exists only if the integral converges.
2. All integral transforms are linear: this stems from the linearity property of the integral itself. Therefore, for a given function space, applying an integral transform on every member of that function space would also give us a function space.

The Laplace transform

We finally come to the Laplace transform: for the laplace transform, the kernel is $K(s,x)=e^{-px}$ and the limits are $x_1=0$ and $x_2=\mathrm{\infty }$. Plugging this into the general integral transform gives us the laplace transform:

$$\boxed{{\displaystyle \mathcal{L}(f(x))=F(p)={\int }_0^{\mathrm{\infty }}{e}^{-px}f(x)dx}}$$

Another bit of intuition regarding the laplace series comes from thinking about it as a continuous version of a power series. If we consider the power series

$$F(x)=\sum _{n=0}^{\mathrm{\infty }}f(n)x^n$$

The continuous analogue of this power series is the integral

$$F(x)={\int }_0^{\mathrm{\infty }}f(t)x^{t}dt={\int }_0^{\mathrm{\infty }}f(t){\left(e^{\ln x}\right)}^{t}dt$$

For this integral to converge, $\ln x<0$. Let $p=-\ln x,p>0$. The transform then becomes

$$F(p)={\int }_0^{\mathrm{\infty }}f(t)e^{-pt}dt$$

Therefore, the laplace transform is like a continuous analogue of the power series.

Further reading

I haven’t covered the several properties of the laplace transform: those specific details can be found on the Wikipedia page. This was mainly to give an overview of the mathematical backbone that goes into transformations such as the laplace and fourier transforms.

For further reading on function spaces, see Vipul Naik’s notes and Terry Tao’s notes on the same. More on laplace transforms (including problems) are given in George Simmons’ Differential Equations with Applications and Historical Notes, chapter 9.

¹No, it wouldn’t. This is analogous to having $\overrightarrow{0}$ as an element of a vector space: if a vector space doesn’t have $\overrightarrow{0}$, then it’s not a vector space as there is no element $k\in V$ such that for every element $v\in V$, $k+v=v$.