The Package Merge Algorithm

This was adapted from a short twitter thread on the Package Merge algorithm I had written, and how it can be applied to create length-limited huffman codes

Problem Statement

Say you’re a broke coin collector. You have some rare coins of denominations 0.25, 0.5 and 1, and need to use them to buy something of total cost 2. We’ll call this the coin collector problem.

Because these are rare coins, each coin also has some value unrelated to it’s denomination. You want to select a subset of coins such that the sum of their values is minimized and their denominations sum to N

The algorithm itself

The Package merge algorithm provides an optimal solution to this problem: group the coins based on their denomination, then sort each group based on value. Then, pair up the least valuable coins with each other.

In the above example, if I have the following values:

0.25 : 1, 2, 3, 5
0.5  : 2, 4
1    : 8, 10

I would pair up as follows:

0.25 : [1, 2], [3, 5]
0.5  : 2, 4
1    : 8, 10

After pairing up, ie ‘packaging’, we ‘merge’ these packages into the next list, sorting by the value of the packages

0.5 : 2, [1, 2], 4, [3, 5]
1   : 8, 10

We then package and merge once again to get all packages of denomination 1

1  : [2, [1, 2]], 8, 10, [4, [3, 5]]

Now we pick the coins/packages of coins with least value (here [2, [1, 2]] and 8) and use them to buy what we want.

I left out some details to simplify things. If an odd number of coins are present in a stack, you discard the topmost one. Also, the denominations must be a multiple of each other so that you can sum and merge them (this is the binary coin collector problem, rather than the generalised coin collector problem)

Connections to Huffman Coding

Making a limited-length huffman code (one where the length does not exceed a certain bound) can be reduced to the package merge algorithm (proof here: https://ics.uci.edu/~dan/pubs/LenLimHuff.pdf). A worked example is given below:

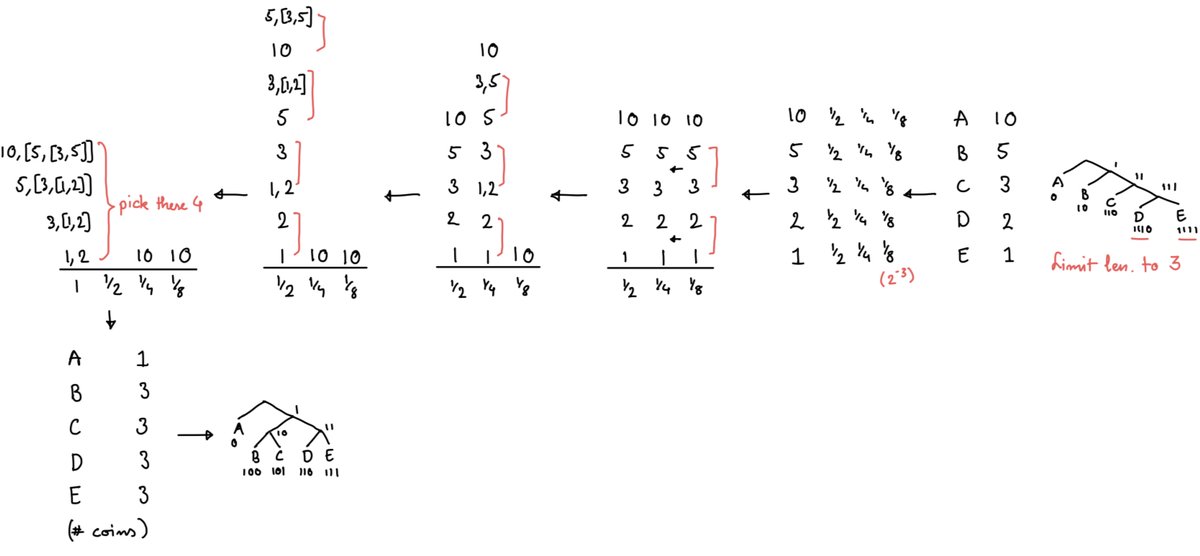
While package merge is optimal, a heuristic way to length limit a given huffman code is to use kraft’s inequality, and the two-pass algorithm described here. What this algorithm does is truncate the longer code lengths, and then do two passes to ‘fix up’ the remaining codes, by increasing and decreasing their length so that kraft’s inequality is maintained.

I came across these algorithms while (re)implementing DEFLATE from scratch following Gary Linscott’s amazing blog. Also, thanks to @sighmoid for encouraging me to write this up :)