Variance Estimation

Motivation

Most linear regression models assume

The standard closed form for this, obtained via finding the MLE estimate, gives , where is the example matrix of shape and is the label vector of shape . Note that is the number of training examples and is the number of features.

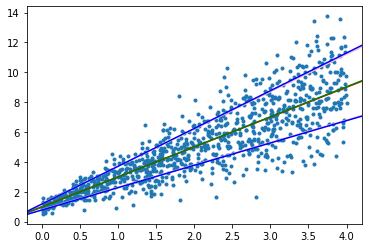
However, the variance need not always be constant. Consider a model where the variance is varying linearly (or rather just increasing) with : an example would be the House prices dataset

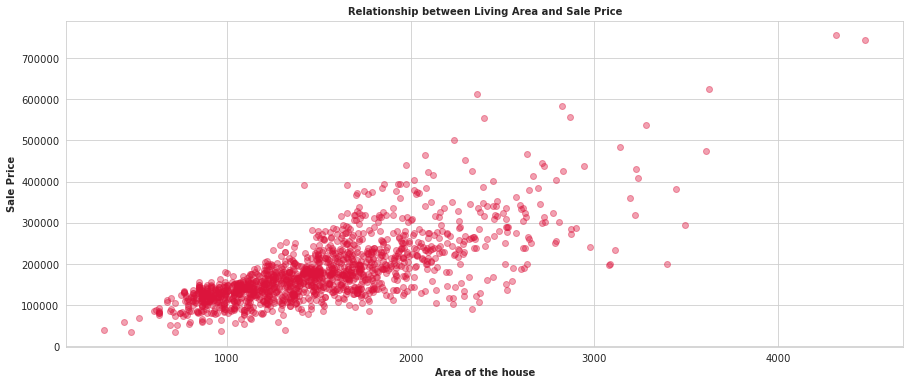
While there are feature transformations that would make this less heteroscedastic, this article focuses on learning the variance parameters, so along with our regression estimate, we can provide a variance estimate as well

The Model

We assume that the standard deviation (not variance) is a linear function of

The log-likelihood function is hence

Differentiating with respect to gives us the gradient for :

Rearranging this gives us, in a matrix form,

Where is our example matrix, is the sum of squared error vector and is the standard deviation vector. This is a nice, concise form that we can use in our code. However, because of the term in the denominator, I couldn’t obtain a closed form for this, and had to do gradient descent on the parameters. Even getting into second derivative methods was getting a bit tedious. If you do find a closed form, let me know :)

The derivative with respect to is pretty standard: we get

An Implementation

Implementation was fairly straightforward, using gradient descent, and it converged nicely to some generated data