| Task | #12 |
|---|---|
| Position | 4 |
| Score | 137,087 |
| Best Score | 110,842 |
| Points | 0.809 |
Problem Statement
You have a data stream of arithmetic expressions to STDIN. Each line has one
expression. The expression contains 50’000 int16 numbers, basic
operations:+, -, *, / - integer division and (, ). For example:
-19550 - ((-14208 / (13583 + -19215)) + (-16832 / 797 + (9060 / -23627)) + ((-6060) + 24953))
30835 - 3703 - (-20089 * -6261 + ((-28985 - 29627) + (-17828 - (22773 / -4014) * 1630)))
-14543 + (-12094 / -20726 + 25651 + (13732 - (28133))) * (1504) + -16348 + (-18371 - (-5750))
(14025) * 12700 + 14455 + ((25584) * -2310) + (27213 + (20470 + -14644 / 1949 / (-20039)))
(-21888 - 15779 - -2220) / 16967 + (20044 + -106 * ((10741 / -9574) * (-28909 - 3737)))
The number of rows is 100.
Evaluate each expression and print the results to STDOUT for the shortest time. The result has int64 type.
Input Generator
This was probably the hardest input generator to reverse engineer. My reverse engineering process went something like this:
- Find a set of distributions that can be obtained from the input that you can fit your generator against.
- Create a hypothetical generator
- See if the generator’s distributions fit
- If they don’t, make them fit by tweaking params, or by creating a new generator
- If they do, find more distributions to fit against
I had to write a modular recursive descent evaluator for 1, which supported adding properties as a pass of the tree. You can find this code in parser.hpp. As a bonus, it’s modern C++, so it has nice algebraic types and pattern matching. Submitting probe.cpp will print the statistics out to stderr so you can copy and analyze them.
Once I did this enough times, I got the following 18 distributions to fit, and my generator fit the important ones reasonably well. The operation distribution means line up, but the variances are a bit off. I’m not too concerned, considering they’re in the same ballpark. I think distribution over depth matters way more than variance, and if we generate a couple more +/- it’s okay. Maybe division causes a larger hit because idivs are expensive, but I don’t think it’s worth optimizing that since I’m not able to get much edge out of this reverse engineering.
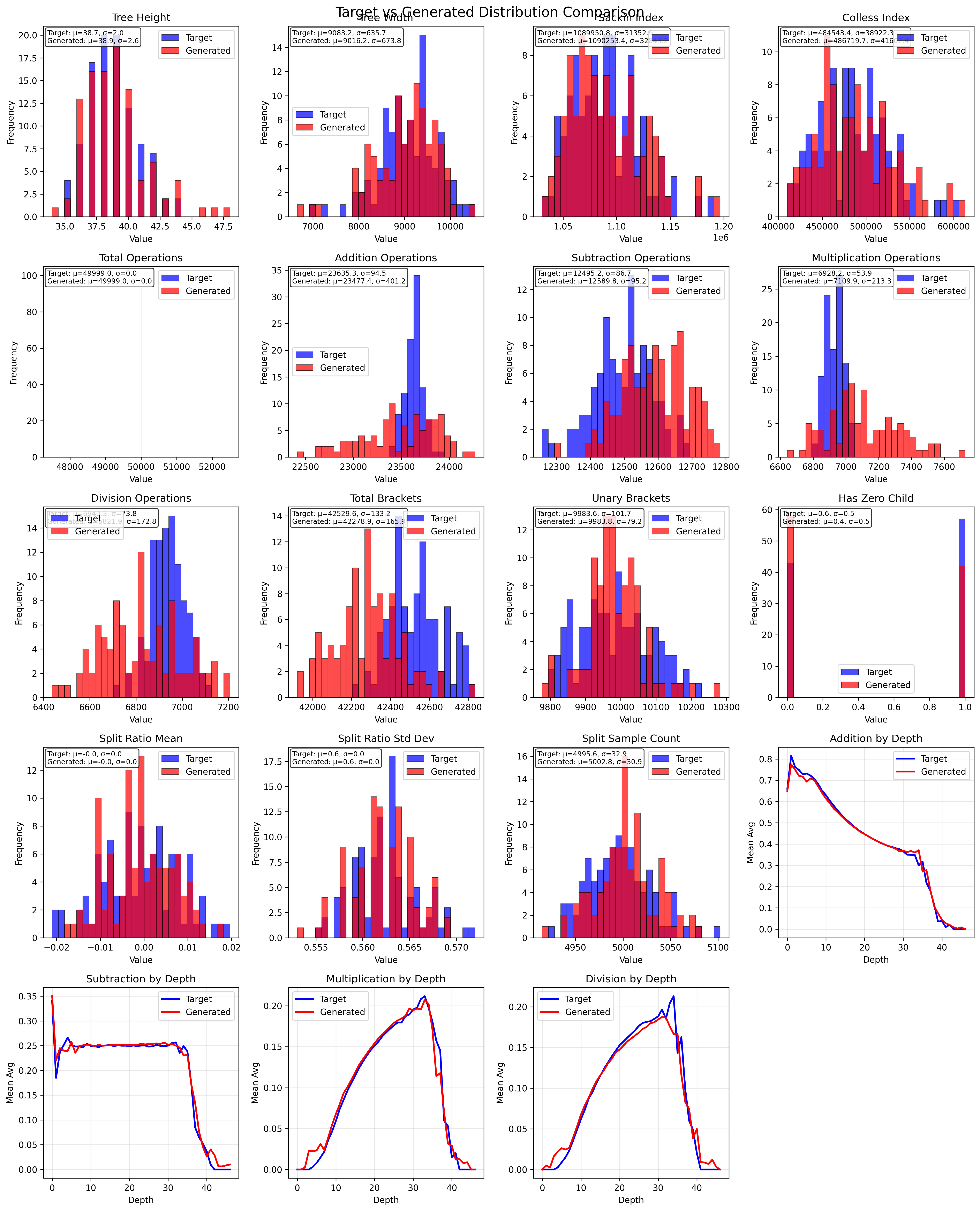
Algorithm
def generate(depth, n_terms):
if n_terms == 1:
if should_parenthesize_single_term():
return "(" + generate_number() + ")"
return generate_number()
split = generate_left_subtree_size(n_terms)
left_expr = generate(depth+1, split)
op = generate_op(depth)
right_expr = generate(depth+1, n_terms - split)
while (evaluate(right_expr) == 0 and op == DIV):
right_expr = generate(depth+1, n_terms - split)
if should_wrap(left_expr, op):
left_expr = "(" + left_expr + ")"
if should_wrap(right_expr, op):
right_expr = "(" + right_expr + ")"
return left_expr + op + right_expr
A couple other algorithms were tried, such as the following PCFG:
E -> UE | (UE)
0.15 0.85
UE -> E + E | E - E | E * E | E / E
0.472 0.250 0.139 0.139
After 50,000 E’s were generated, everything would be converted to UE’s (Unparenthesized Expressions). This did not satisfy the balance properties of the tree, which I estimated through the sackin and colless indices.
Solution Sketch
I didn’t do anything special for this challenge. Just used shunting yard, stacks with swap front instead of push/pop, a SWAR-based integer parsing algorithm, and a lookup table to determine precedence. Kept the lookup table’s size small by measuring offset from ( instead of the character value itself.
Fast tokenization/SIMD tokenization: I tried implementing this master thesis on fast lexing using SIMD/SWAR; it’s similar to simdjson in how it detects whitespace, but it does aggregation using PEXT. This should be slightly better in terms of branch prediction, because you know sequentially what the next token you process will be instead of jumping around. It was not.
Some other observations you can use:
- Operations are always padded with spaces around them. You can use this to optimize your parsing.
- After processing a left brace, the probablility the next char is a left brace is quite high, so try to consume as many left braces as possible at once. If you can’t, the next token is always a number, so go to processing a number.
- If you profile this,
idivs take up most of the time. I tried optimizing those away with some branches + casework, but that ended up being slower than the idiv.
I could not find ways to exploit the generator’s expression structure, sadly. That time would’ve been better utilized throwing ideas at the evaluator and seeing what sticks.
Thoughts
I don’t think there are algorithmic improvements to be obtained here, maybe something with division can be done better. Parsing can be done better, I got a bit lazy with it once the paper didn’t work and did not explore more.