Large Integer Multiplication

Task	#20
Position	1
Score	8,326
Best Score	8,326
Points	1.000

Problem Statement

You have a data stream of exactly 500 000 bytes to STDIN. Encoded in the stream are two unsigned integers. Each integer is exactly 250 000 bytes, and they are encoded back-to-back. The byte order is little endian.

Compute the multiplication of these two unsigned integers. Write exactly 500 000 bytes to STDOUT, containing the result in little endian byte order.

Input Generator

it’s not uniformly distributed integers. Distcheck fails with p = 0.030827 for 256 bins, which are plotted below.

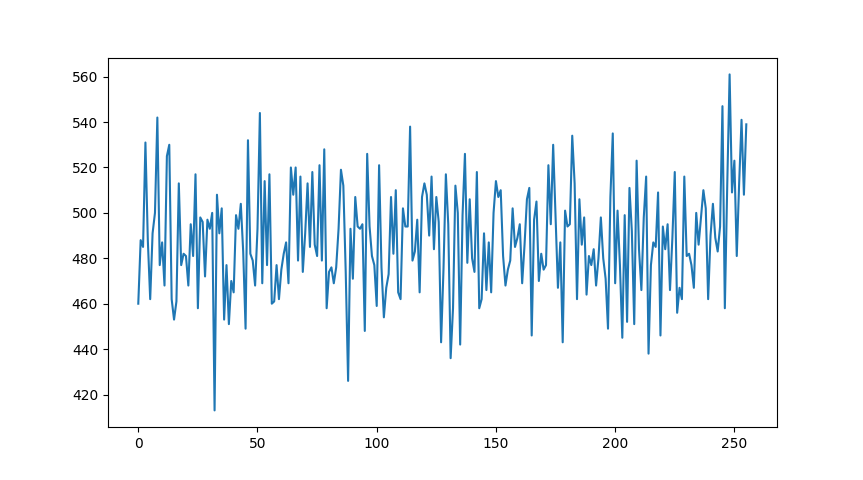
There’s more values towards the upper range of uint32_t. My guess is this is to require carry propagation till the end (eg multiplying 123 * 123 = 015129 vs 789 * 789 = 622521. Both have 6 digits in the answer, but the former’s leading digit is a zero.)

Solution Sketch

Say you have two numbers in base 10. You want to multiply them, but you don’t have a multiplier. You only have a function that will give you the pointwise convolution of two vectors, i.e.

How would you multiply 12 and 34 using the convolver?

Solution

let and . Then, . However, if you convert back to base 10, and propagate the carries, you’d get , which is the answer!

If you’re not convinced multiplication is convolution with carry propagation, then try doing it for 123 and 456

If we know how to express multiplication as convolution, our problem has gone from being to because we can use the FFT for convolution! There’s just one small issue. So far, we assumed is arbitrary precision. Unfortunately, real life is not so. Let’s say we have a fast approximation:

We can still do this in for ‘nice’ M (it’s called the Number Theoretic Transform. It’s basically FFT, but using roots of unity in instead of ).

There’s an issue with this: if your coefficients exceed M, they’ll effectively be ‘chopped off’. A suitable value of M we can use for fast NTT is 998244353, which is 119 * 2^23 + 1. With two 250kB integers (~2^18 bytes) and 8-bit limbs (ie base-256), our largest coefficient will be - this will overflow! Let’s use 4-bit limbs then, giving us a max coeff of .

This solution is good enough for second, where I sat for a long time until Yuriy passed me. The issue with this solution is that 4-bit limbs require us to use a NTT with terms. That’s a lot of work, and the NTT was taking the majority of the time (not carry propagation/widening), even though I was using the fastest one on yosupo

To speed this up, we need to use larger limb sizes. A 16-bit limb size shortens our NTT to terms. What if there was a way to reconstruct the data we lost in the modulo? Since with 16-bit limbs we do a quarter of the work, let’s multiply twice with two primes; we’d still be doing half the work.

Since and are coprime, we can use the chinese remainder theorem to construct mod using and . This increases our range to , and we can use 16-bit limbs in both multiplications. The range will be on each multiplication, which will clip, but we’d get a distinct c after recombining (which we’ll do in 64 bits now, instead of 32 bits). The CRT step itself is not too compute intensive; it’s just multiplication with a modular inverse, which we can do via SIMD montgomery, which the fft also uses

Once we have , add and carry propagate to get the final answer.

Thoughts

The real trick to being #1 was using a really fast NTT. qwerty1232 (the author) explained how he vectorized the NTT in this brilliant CF blog.

Another solution would be to just use a fast double-based FFT with large limb sizes, which adamant says is not too bad. I tried this, and got a score ~21k, so it wasn’t as effective as CRT+NTT

Schonhage-strassen is the canonical bigmul algorithm, but that operates only in a ring, with some nice recursion logic to stay in that ring when products are recombined. There’s a nice paper on how this was implemented in GMP, but reading the source and looking at the implementation shows that it’s not quite vectorized (impl in mpn/generic/mul_fft.c. I don’t know if this NTT+CRT solution is faster than GMP yet.