Aniruddha Deb

Unique Strings (v2)

7 min read

Task#7
Position7
Score269,976
Best Score128,516
Points0.476

Problem Statement

You have a data stream of string tokens to STDIN. Each line of the flow has one token. The token is a combinations of chars from the set 0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ@#%*. The maximum length is up to 16 chars. For example:

JWXcKKaWzvFL5
Rof
3ztCpA
5wHcGN
*UiEMthaTS*g

The number of unique tokens is about 1,000,000. Try to find the exact number of unique tokens for the shortest time.

(for v2, you have 3 CPU cores, and the score function is wall time)

Input Generator

Parameterize the input generator as a random function , where is the th generated string, and is the set of unique strings at time . Therefore, our function is only dependent on the number of unique strings and total number of strings that have been generated so far. We also know that is a string taken from the specified alphabet set, and we assume that every character of is uniform randomly generated.

To fit this function to the input generator, we’ll need to get information about these distributions:

  1. Distribution of over , i.e. are all string lengths equally likely
  2. The probability that is unique, as a function of

The first one just needs us to bucket over length:

Length counts: 
0: 0
1: 2518
2: 170475
3: 2073504
4: 2306013
5: 2331668
6: 2301950
7: 2310433
8: 2313199
9: 2313132
10: 2313289
11: 2311427
12: 2311345
13: 2314488
14: 2315956
15: 2310603
16: 0

Interesting that there are no strings of length 16, and fewer strings of length 1,2,3. Which is understandable, since our alphabet is only 66 characters. The number of unique strings we find in each bucket are:

Unique Length counts: 
0: 0
1: 66
2: 4339
3: 69189
4: 78742
5: 79286
6: 79662
7: 79410
8: 79900
9: 79349
10: 79186
11: 79385
12: 79297
13: 79669
14: 79692
15: 79108
16: 0

So bucket 1 is saturated and we can skip all strings of length 1, bucket 2 is almost saturated (66^2 = 4356), and bucket 3 is slightly lower than others. For the rest, it’s a uniform distribution.

The second hypothesis above needs us to bucket unique occurences over time:

First occurences over time counts, units=1M
0: 534168
1: 134740
2: 40049
3: 17945
4: 12716
5: 11746
6: 11063
7: 11241
8: 11124
9: 11166
10: 11088
11: 11200
12: 11095
13: 11321
14: 11182
15: 11190
16: 11057
17: 11064
18: 11034
19: 11256
20: 11085
21: 11301
22: 11305
23: 11090
24: 11157
25: 11160
26: 11056
27: 11240
28: 11037
29: 11228

We see that more than half of all unique strings occur in the first bucket, and then the distribution falls off exponentially. This continues to be the case if we zoom in further on the first bucket:

First occurence over time counts, units=100k
0: 93171
1: 80814
2: 70404
3: 60914
4: 52604
5: 46021
6: 39631
7: 34732
8: 30141
9: 26323
10: 22800
11: 19662
12: 17474
13: 15253
14: 13239
15: 11703
16: 10239
17: 8819
18: 7934
19: 7118
20: 6231
21: 5572
22: 4934
23: 4467
24: 4076
25: 3566
26: 3228
27: 2991
28: 2788
29: 2580

So we know that the probability of generating a unique string decays exponentially.

Putting these two together, can be modeled as follows:

def generate_string(U, length):
	if length <= 3:
		# pick the next string from a randomly shuffled pool of all possibilities
		# if we're out of possibities (eg len=1), generate a duplicate
	else:
		random_string = generate_random_string(length)
		while U.contains(random_string):
			random_string = generate_random_string(length)
		return random_string
 
def f(U, t, N=30_000_000, k=7.85 * 5.5):
	length = sample_discrete_uniform([0.0012, 0.074, 0.896] + [1.0]*12)
	p_uniq = p_baseline + (1-p_baseline)*exp(-k*t/N)
	if sample_bernoulli(p_uniq):
		new_string = generate_string(U, length)
		(new_string, U.add(new_string))
	else:
		(sample_random(U), U)

There’s a full implementation in C++ here with the right constants, and I’ve matched it to the HighLoad generator’s distribution as closely as I can.

There is always the off chance that a better parameterization will yield something that fits the generator better with fewer parameters (ie is less overfit). If you do find something, let me know and I’ll update my generator.

Solution Sketch

At a high-level, my solution is:

  1. Parse and hash all input strings, and bucket based on string length
  2. For each bucket, count the number of uniques

Part 1 can be parallelized with some effort, by maintaining three memory regions and doing a merge. Part 2 is trivially parallelizable with #pragma omp parallel for. Since it’s so easy to parallelize, I have the same solution for both, and the forthcoming explanations of the parts refer to the same, single solution.

Both parts as implemented take roughly the same amount of time. I’m sure that my parsing is super sloppy and can be improved, it should not take so much time.

Parsing

SIMD compare, generate a movemask, shift and pop to extract strings. For each string, truncate to the first 8 characters, hash and push to the right buffer based on the length. I think appending to the buffer based on length is slow, and incurs a lot of thrashing, but I haven’t done a deep dive.

Unique counting

I use a simple table with an n-bit index and a m-bit value. For a hash H with atleast n+m bits, the index is the lowest n bits and the value is the highest m bits. With a good hash, this order does not matter, ie you can swap it around and let the bottom m bits be value and the next n bits be index.

To insert, probe the index. There may be three cases for the value stored at the index:

  1. If it equals the value being checked, it’s a duplicate.
  2. If it’s 0, insert the element and increment the count of unique elements.
  3. For all other cases, we have a collision.

Note that if we inserted 0 at index k and then try to insert v at index k, it should be a collision, but since we use 0 as the empty slot indicator we’d count a false positive (something that’s not a unique element but is counted as if it is one). This is bad luck, and with a large enough value of m given the constraints of this problem, this never happens in practice.

If we have a collision, push the hash into an ankerl::unordered_dense::set. The final answer is the count of elements in the table, plus the count of elements in trickles.

To select m and n, Increasing n will give you fewer collisions, but under the constraints of this problem you need an address space of 39+ bits to have no collisions, so purely trying to reduce collisions is not a good strategy.

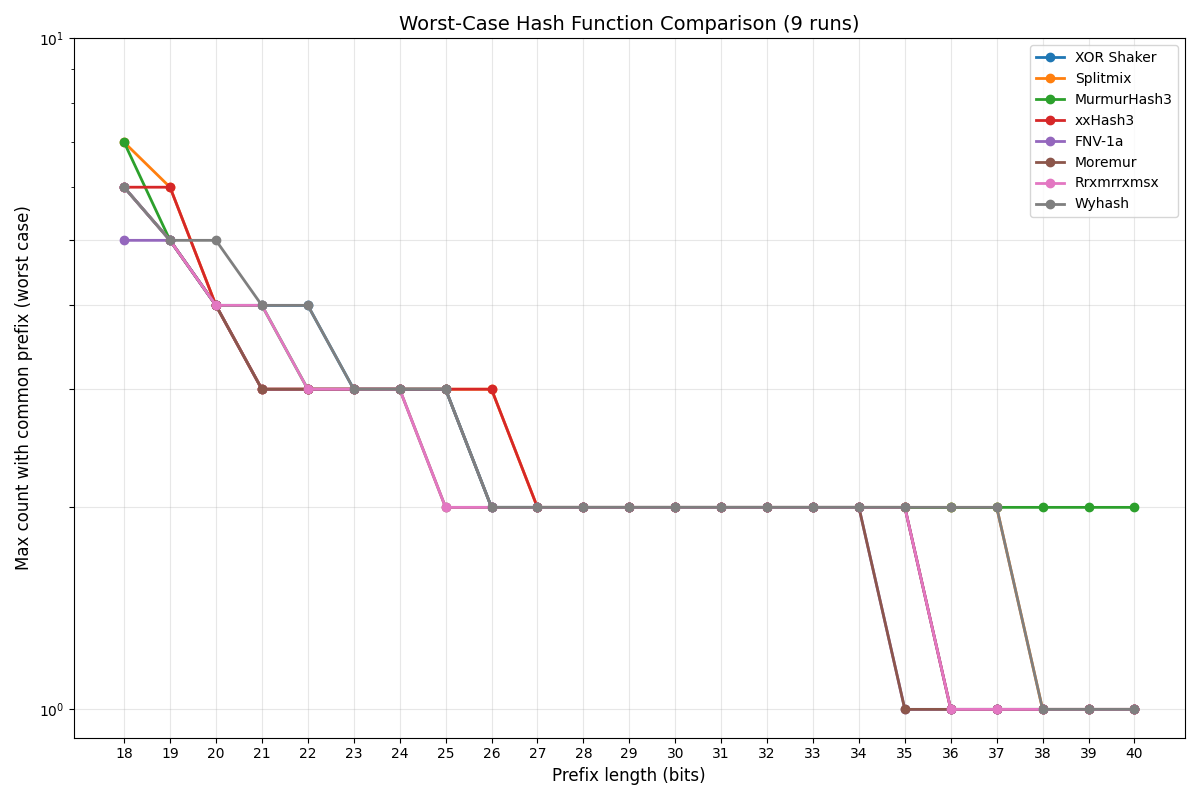
worst case

The graph above is what I used to set constraints. We want m+n to be such that there are no false positives, and n is as high as possible to reduce the number of trickles we have to handle. This gives n = 20 and m = 32 as reasonable constraints. m has to be a multiple of 8 so comparision is word-based.

I’ve tried quite a few other data structures (swiss tables, cuckoo filters) and probing techniques (linear, quadratic, robin hood) but this structure wins against them. Most of my testing was on a prior solution that found all the duplicates in one pass instead of partitioning by length though, so there’s a chance another data structure wins on the smaller amount of data we need to process when bucketed by length. Considering I’m not first, I’d say this is true.

Thoughts

This is a really good problem because there’s a lot of other problems that can come out of it, combined with not many resources being available online and a sparse leaderboard. Zielaj recently went under a 100k, and there’s still edge to be found in the parallel formulation. It was also a fun problem to hunt down the generator’s formulation, maybe more than I had solving the problem itself.

I think there are some fancy 80/20 tricks that can come out of the generator’s structure, such as precomputing a faster duplicate check filter after processing the first 2M elements and using that on the following 28M elements to speed up checks.

Graph View

Backlinks